|
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
 |
■入試数学の本格的な対策問題集として改訂を重ね、第5版となる、「入試図形問題の攻略Version5<247問>」です。今回のバージョンでは、いままでとガラリと構成も企画も変更しました。問題数は前回の216問から247問へと増やしましたが、それ以上に、従来の公立トップ高を目指している生徒へのご利用はもちろんのこと、もっと幅広い生徒に、入試数学でもっとも重要となる図形力の向上が具体的に図れるよう、根本的に編集し直しました。 生徒が問題を解いたあと、当然解けなかった問題がいろいろ出てきます。その問題に対し、誰の手も借りず生徒自身の頭で考え、如何に解けばいいのか、そして解法のポイントはどこでどう押さえて覚えていれば次のとき解けるようになるのか、これらのことが解答編では、つねに解説とポイントで詳しく書いています。また、覚えていれば大変役立つ公式も明記し、長い計算式も省くことなく書いています。 深く理解できるのはもちろん、重要な知識や解法テクニックをしつこく盛り込んで作ってありますので、似た問題のくり返し学習によって、単にわかるから「できる力」の養成が間違いなく図られることでしょう。 |
| ■ 価格:18,000円(代引きで送料、消費税込みの価格です) ■ 配送方法:「代引き」でのゆうパック便(手数料260円別途)です。 ■ 納品予定:ご注文より、2,3日以内に着くよう手配。 |
■ お申し込み:ショッピングカートで、スタートボタンを押し、 「入試図形問題の攻略 Version5」をクリックしてして下さい。 こちらからでも受付→ |
|
||||
| ◆入試図形問題の攻略 Version5 <247問>の構成 | |||
| 学習項目 | プリントNO | 問題数 | |
| 1 | 応用の基礎知識(平面図形・空間図形) | NO.1〜NO.22 | 50問 |
| 2 | Aレベル(平面図形)★と★★問題 | NO.1〜NO.35 | 62問 |
| 3 | Aレベル(空間図形)★と★★問題 | NO.1〜NO.28 | 44問 |
| 4 | Bレベル(平面図形)★★と★★★問題 | NO.1〜NO.22 | 26問 |
| 5 | Bレベル(空間図形)★★と★★★問題 | NO.1〜NO.12 | 14問 |
| 6 | Cレベル(平面図形と空間図形)★★★★問題 | NO.1〜NO.8 | 8問 |
| 7 | 動点・図形移動問題 A・Bレベル | NO.1〜NO.12 | 13問 |
| 8 | 2次関数 A・Bレベル | NO.1〜NO.18 | 18問 |
| 9 | 入試図形問題に対する実力確認 | NO.1〜NO.10 | 12問 |
| 各問題レベルの参考として、問題集の解答編では下の印をつけています。 無印: 教科書レベルの基礎知識があり、その運用がふつうにできていれば、まず解ける問題です。 ★印: 入試応用問題のなかの基本レベルに位置し、確実に解けるようにしておくべき問題です。 ★★印: 応用に関するさまざまな知識と解法のテクニックなど身につけていなければ、解けない問題です。正答率は3%から8%です。 ★★★印: 応用問題のなかの上ランクに属する問題、いわゆる難問です。正答率は3以下です。 ★★★★印: 正答率1%未満の超難問です。 |
|||
| なお、また上記を偏差値に置き換えてみると、次にような感じになります。<注:ただし、ここでの偏差値は、業者の有名模試を想定してその基準で書いてみます。公立トップ高のレベルは、偏差値68から72とします。 (ネット上で表現されている偏差値はどうもインフレ気味で一般に高過ぎます。> 無印: 偏差値50〜59 ★印: 偏差値60〜63 ★★印: 偏差値64〜67 ★★★印: 偏差値68〜72 ★★★★印: 偏差値73〜75 |
|||
| ■1.「応用の基礎知識(平面図形・空間図形)」の学習内容(50問) |
| この「応用の基礎知識(平面図形・空間図形)」では、入試図形問題を解いていく上で必要とする目線の持ち方と思考の手順、また重要な解法のノウハウとテクニック、そして暗記しておいて活用すれば、極めて有効な公式(学校では習わないもの)など、これらをまず演習し習得するために用意したプリントです。 A,B(C)レベルの入試図形問題を解いていくために元となる欠かせない図形力の知識とノウハウが入っていますので、しっかり身につけてみてください。 (なお内容はすべて、応用の基礎とはいえ教科書レベルの基礎や基本ではなく、入試問題より抜粋・構成しており、★と★★レベルまでの問題を含んでいます。) |
| ■2.「Aレベル(平面図形)★と★★問題」の学習内容(62問) |
| この「Aレベル(平面図形)」は、大問設定なので無印もありますが、小問後半部分で出てくる、教科書レベルの知識や学力だけではまだまだ対応しきれない図形力を補強し、また入試問題の応用に向けた知識やノウハウをこのプリントで吸収し具体的にかつ実践的な運用をすれば、まず解けるレベルの★の問題と、これよりやや高度になる★★までの問題を中心に構成しています。 問題枚数は35枚、問題数は62問と問題集のなかでは一番の量があり、入試対策の勉強としてはこれ以上のものは必要ないでしょう。また、3から6の問題でもしつこいほど演習しますが、証明問題の対応にも万全になっていくことでしょう。 |
| ■3.「Aレベル(空間図形)★と★★問題」の学習内容(44問) |
| この「Aレベル(空間図形)」は、大問設定なので無印もありますが、小問後半部分で出てくる、教科書レベルの知識や学力だけではまだまだ対応しきれない図形力を補強し、また入試問題の応用に向けた知識やノウハウをこのプリントで吸収し具体的にかつ実践的な運用をすれば、まず解けるレベルの★の問題と、これよりやや高度になる★★までの問題を中心に構成しています。 問題枚数は28枚、問題数は44問とです。入試数学の空間図形問題の解き方の定番的パターンをこれで勉強してみてください。平面図形とともに空間図形にもかなりのレベルまで対応できる力、そして攻略できる力が身につくことでしょう。 |
| ■4.「Bレベル(平面図形)★★と★★★問題」の学習内容(26問) |
| この「Bレベル(平面図形)」は、Aレベルを勉強して手応えを感じた生徒が、さらにワンランク上の入試図形平面問題を演習し身につけるために用意したもので、★★と★★★レベルまで含んだ問題となります。 実際、★★レベルの問題が確実に解けるようになれば、たとえ公立トップ高でも合格圏内に入る入試数学の学力となりますが、さらに★★★レベルまでの図形力を磨いていくために、このプリントを演習してみてください。問題枚数は22枚、問題数は26問です。 |
| ■5.「Bレベル(空間図形)★★と★★★問題」の学習内容(14問) |
| この「Bレベル(空間図形)」は、★★の問題も引き続きありますが、さらに一段上の★★★レベルの問題を含んだ構成になっています。立体図形をどういうふうに観て切り込んでいけばいいのか、どういうテクニックを使って解き進めていくのかは、Aレベルの問題でじゅうぶん養ってきているはずですが、ここではさらにその力をブラッシュアップしてみてください。問題枚数は12枚、問題数は14問です。 |
| ■6,「Cレベル(平面図形と空間図形)★★★★問題」の学習内容(8問) |
| この「Cレベル(平面図形と空間図形)」は、★★★★問題として特別に8問だけ用意しました。本来、入試図形の応用問題として、ランク的にこの問題集では★★★が最高で、これがもしできれば、公立トップ高のなかでも数学に関しては、文句なく上位の成績がとれるはずです。 ですので、ここの問題はほとんどの生徒の場合、無視してもらって取り組まなくてもいいですし、またたとえやってできなくてもまったく構いません。あくまで+αとして、超難問に興味のある生徒だけトライしてみてください。 |
| ■7.「動点・図形移動問題 A・Bレベル」の学習内容(13問) |
| この「動点・図形の移動問題」は以前に較べ、入試に出る割合は、規則性や数学的思考力を要する問題が増えてきたため減ってきました。しかし、大事な問題群として必ず解法できるよう習得しておかねばなりません。2次関数との絡みで出題されることが多いです。 苦手とする生徒は多いですが、慣れてしまえばそれほど難解な問題はありません。思考のパターンとしては定番的に解けるので、そのへんをこの13問で習得してみてください。ポイントは、距離、折れ曲がってもUターンしてもx(エックス)でそのまま表せる、そして相似を使うということ。このふたつです。 |
| ■8.「2次関数 A・Bレベル」の学習内容(18問) |
| この「2次関数」編は、特別に追加したものです。というのも、入試問題で問われる2次関数の問題は、図形の知識が必要で、かつ図形絡みで出題されることが多いからです。 生徒の感覚とは異なりますが、1次関数も2次関数もさして高度な応用問題というのはありません。95%以上の問題は、応用とはいえAレベルorBレベルの★から★★★までのしかも定番的な問題です。 ですから解法のテクニックやノウハウを、ここに出題した18問で学習し吸収すれば、公立はもちろん私立の問題にもじゅうぶん対応できますので、そのつもりでやってみてください。 |
| ■9.「入試図形問題に対する実力確認」の学習内容(12問) |
| この「入試図形問題に対する実力確認」のする時期については、ふたつあるかと思います。 ・ひとつは、上記1から8までの内容をほぼ済ませてから最後に、自分の図形力がどのくらいついたのか、その確認の意味でこのプリントすればいいですね。(こちらが基本です。) ・もうひとつは、中3課程の数学を学校や塾で一応終えたあと、入試数学のそれも数学の実力差が如実に出る図形問題に対して、ます自分の力がいまどの程度あるのかを知るために、そしてこれからどのように入試に向けた知識やノウハウを学び習得していかなければならないのかを実感するために、このプリントをはじめに取り組んでみてもいいですね。 |
| <注>入試数学図形問題の先行学習をやりたい生徒で、しかしまだ「中3の因数分解、平方根、2次方程式」の特に計算に関する勉強をしていない生徒のために、下のプリントを別に用意しています。 「Aの相似の基礎知識(NO.1〜9」と「Bのの三平方の定理を解くための基礎計算(NO.1〜11)を勉強してから、じっくり時間をかけて「入試図形問題の攻略ersion5」に取りかかってください。これは別売(1,000円)です。 |
|||||||||||||
|
| 応用問題ができるようになるための必要な知識とノウハウ習得の演習は、この問題集でしっかりやります。しかし、教科書や授業にある基礎とそのまわりにある、さして重要とはいえない知識や問題に関する演習はしません。学校の定期テストではたとえ90点以上とれていたとしても、入試の図形問題になると、50点くらいの学力しか身についていなかったってことがめずらしくないからです。 それゆえ、この図形問題集は、入試での点数に大きな差が出る、そして最大のポイントになる図形問題(関数問題も入れてあります)に対して、いったいどうしたら入試レベルの応用問題を解き進める能力が身につけていけるのか、また思考力を鍛え応用問題を解く技術を学べていけるのか、そこに焦点を当て、この難しい課題と目標に向かって作られた問題集です。 入試数学のなかで極めて大きな比重を占める図形問題というものは、過去3カ年や5カ年の過去問を解き、その対策を塾でやったからといって、その他の問題と違い、すんなりとそのまま生徒の実力向上に反映したり、確実にできるようになることはまずあり得ないのが、大多数の生徒の実情です。 ここでもっとも大事な勉強のしかたは、生徒個々人の能力に合った図形問題追及の勉強です。 入試数学の図形問題(平面図形も空間図形も)は、よくご存じのように、一般に大問のなか小問が3つあるいは4つに別れて出題されています。ここでは4つとして書いていきます。たいてい順番に難しくなっていきます。 小問4問構成のケースでは、たとえば小問(1)はほぼ無印のレベル、,(2)は証明問題として無印か★レベル、,(3)から★★という応用の中ランクの問題、そして最後(4)になると★★★レベルの難問になります。ただなかには、(1),(2),(3)ともあまりにも平凡で基本レベルなのに、最後の(4)になると突然何を思ったか豹変して急激に難しい問題構成になっているケースもあり、また(1)だけは基本的証明でやさしく、(2)からあとじわじわ難しい問題設定になっている場合もあります。(しかし近年、公立入試のこの鉄則がぶち壊され、小問1番あるいは2番からいきなり思考力を要する高いレベルの問題を出す県もごく一部出てきましたが・・・。) さて、生徒にとって応用とは、どういうふうに感じ捉えているのでしょうか? 私が問題集で分類している無印も実は、教科書的な基本知識というよりも入試レベルの基本であり、かつ偏差値的には50から60までに相当しますので、ある生徒にとっては応用と感じることもあるでしょう。また、★ひとつでややこしいなあ、応用だなと感じる生徒もいることだと思います。こうした生徒にとっては、まさにここが上記した「生徒個々人の能力に合った図形問題追及の勉強」なのです。このゾーンの勉強を問題集でしてみてください。 次に、★★レベルが問題を解いて難しい、応用だなと感じる生徒は、この下の★をじゅうぶん固めるとともに、★★の問題を徹底して研究し、理解し、解法を習得・暗記することが入試勉強最大のポイントで、入試で確実に点数をとることが求められます。 そして公立トップ高校を目指している生徒の場合、★★★レベルの問題を攻略する図形力を身につけることが目標ですが、実際入試本番でできる確率は50%前後でしょう。ふだんできることが、入試本番では緊張と焦りなどで解けなくなることがあるからです。でも、それでもいいんです。★★レベルがきちんと正解できていれば。そのため、★★問題をじゅうぶん手の内に入れる勉強を行い、そして★★★の問題を十二分に演習してみてください。正答の確率はもうすこし上がるはずです。 最後に、★★★★の問題を今回のVersionでは用意しましたが、これはあくまで付録です。★★★レベルの問題がなんなく解ける生徒だけが、研究追及してみてください。 |
| <最新版>入試図形問題の攻略 Version5 の問題 サンプル | |||
| 下の1から6まで問題プリントをクリックしてもらえば、拡大します。 実物はB-4ですが、A-4サイズ版で印刷、問題ができるようにしています。 |
| 問題編 | 解答編 | |
【1.応用の基礎知識】 NO. |
 |
 |
【2.Aレベル(平面図形)】 NO. |
 |
 |
【3.Aレベル(空間図形)】 NO. |
 |
 |
【4.Bレベル(平面図形)】 NO. |
 |
 |
【5.Bレベル(空間図形)】 NO. |
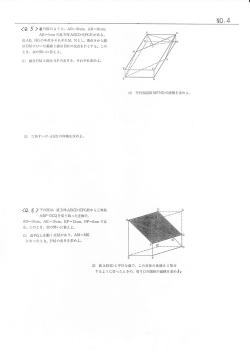 |
 |
【6.Cレベル(空間図形)】 NO. |
 |
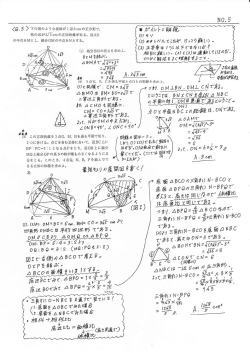 |
| 【7.動点・図形移動問題A・Bレベル】 |
【8.2次関数A・BCレベル】 |
【9.入試図形実力確認】 |
 |
 |
 |
|