| �����������䡡���ꣲ����������������INDEX���������������������2����������3�� | |
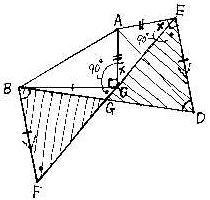
| ���䤤�䲼�οޤǻ��ѷ�ABC�ϡ���ACB��90�٤�ľ�ѻ��ѷ��Ǥ��롣 ���ѷ�ADE�ϡ����ѷ�ABC��ĺ��A���濴�˲�ž��������ΤǤ��롣 ľ��CE��ˡ���F��BC��BF�Ȥʤ�褦�ˤȤ롣ľ��BD��ľ��EF�Ȥ� ������G�Ȥ���Ȥ���EG��FG�Ȥʤ뤳�Ȥ�������衣 |
|
 |
�������٤�ɽ�����Ǥ��ʤ��Τǡ������Ρ��١פ� ���Ѥ��Ƥ��롣���̤Υޥ���٤�Ф褤�͡� |
| �̾����� ��FGB�Ȣ�EGD�ˤ����ơ� �����ꡢ��ABC�ᢤADE�����顢 BC��DE �ޤ���BC��BF�ʲ���� ��äơ�BF��DE�ĭ� BC��BF��ꡢ��BFC�������ջ��ѷ������顢 ��BFG���BCG�ĭ� ��ACB��90�٤�ꡢ��BCG��90�١ݢ�ACE ��AED��90�٤�ꡢ��DEG��90�١ݢ�AEC �Ȥ�����AC��AE�ǡ���ACE�������ջ��ѷ������顢 ��ACE���AEC ��äơ���BCG���DEG�ĭ� ���ȭ���ꡢ��BFG���DEG�ĭ� ���Ѥ����������顢BF��ED ��äơ���FBG���EDG��ʿ�����κ��ѡˡĭ� ������������ꡢ 1�Ȥ��դȤ���ξü�γѤ����줾�����������顢 ��FGB�ᢤEGD �椨�ˡ�FG��EG�����ʤ����EG��FG |
|
| �̲���� ����FBG���EDG���ˤ��ƾ������Ƥ����������줬�ݥ���Ȥ��͡� ���٤⸫ľ���ơ��褯�褯��ʬ��Ƭ������뤳�ȡ� ���Τ��ȡ����ѷ�����Ѥ��¤�180�٤��顢��ĺ�Ѥ�Ȥä��̤����� ���Ƥ�����ˡ�⤢�롣�����ޤDz����λ�����Ȥ��ơ� |
|
| ����ɾ�� ��Ʊ���������ɡ����ä���Ĺ���������פ롣 ���Τ��餤����Ĺ���ξ������Ǥ���С���ʪ�Ǥ��롣 |
|