| �����������䡡����1����������INDEX�������������1����������2�� | |
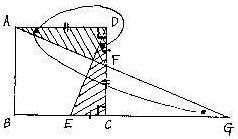
| ���䤤�䲼�οޤΤ褦�ˡ�������ABCD����BC��CD��ˡ�CE��DF�Ȥʤ� ��E��F�줾��Ȥ롣�ޤ�ľ�����Ƥ�BC�α�Ĺ�Ȥθ�����G�Ȥ��롣 ���ΤȤ�����CDE���CGF�Ȥʤ뤳�Ȥ�������衣 |
|
 |
�������٤�ɽ�����Ǥ��ʤ��Τǡ������Ρ��١פ� ���Ѥ��Ƥ��롣���̤Υޥ���٤�Ф褤�͡� |
| �̾����� ��AFD�Ȣ�DEC�ˤ����ơ� �ͳѷ�ABCD�������������顢 AD��CD�ĭ� ��ADF���DCE��90�١ĭ� �ޤ���DF��CE���ʲ���ˡĭ� ������������ꡢ2�Ȥ��դȤ��δ֤γѤ����줾�����������顢 ��AFD�ᢤDEC �椨�ˡ���DAF���CDE�ĭ� �ޤ�AD��BC�������������դ�ꡢAD��BG�����ʤ����Ǥϡ������¹Ԥε���Ȥ���� ��äơ���DAF���CGF��ʿ�����κ��ѡˡĭ� ��������ꡢ��CDE���CGF |
|
| �̲���� ����������ˤ����ʤ�Ԥ��ʤ��͡� �������Ʊ�������̤ˤ狼�뤳�Ȥ�ץ饹�ͷ��� ���ᢤ ���ᢢ ��äơ����ᢢ �Υƥ��˥å��� ��������ʤ��Ȥϡ��������Ȥ������Ȥǡ������դ�ʿ�ԡפȤ������ȡ� ����Ϥ褯�Ȥ��� ����ɾ�� ���줯�餤�Ǥ��ʤ���С�����ξ����Ϥʤˤ�Ǥ��ʤ��ȹͤ��Ƥ⤤�����餤�� �Ǥ������̤ϡ���������2�ء� �Ǥ��ʤ��ä����̤ϡ����˹Ԥ������ޤ����ä������ơ������ƳФ�����ǡ� ���Τ��Ȥǡ�����2�ʲ��ؿʤ�٤��� |
|