| �����������䡡����3����������������INDEX���������������������3������ |
| ���䤤�䲼�οޤΤ褦�ˡ���ʬAB��ľ�¤Ȥ���Ⱦ�ߤμ����AC��BC�Ȥʤ� ��C��Ȥ롣�ޤ�����AC�������D�Ȥ�����ʬBD��AC�θ�����P�Ȥ��롣��A�� �̤ꡢ��ʬAC�˿�ľ��ľ�������������ľ�����CP��AQ�Ȥʤ���Q�� ��ʬCQ��BD�Ȥθ�����R����ʬCQ��AB�θ�����S�Ȥ��롣 ���ΤȤ���CR��BP�Ǥ��뤳�Ȥ�������衣 |
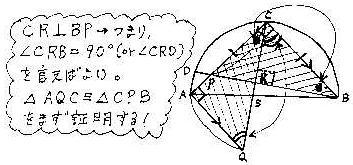 |
| �̾����� ��AQC�Ȣ�CPB�ˤ����ơ� �����ꡢAC��CB�ĭ� ������������AQ��CP�ĭ� ľ�¤��Ф�����Ѥ�90�٤����顢 ��PCB��90�� ��äơ���QAC���PCB��90�١ĭ� ������������ꡢ2�Ȥ��դȤ��δ֤γѤ����줾�����������顢 ��AQC�ᢤCPB �椨�ˡ���ACQ���CBP�ĭ� ����ꡢCB��AQ�����顢 ��AQC���BCR�ĭ� ��������ꡢ ��ACQ�ܢ�AQC���CBP�ܢ�BCR ���ѷ�����Ѥ��¤�180�٤����顢 ��AQC�ǡ���ACQ�ܢ�AQC��180�١�90�١�90�� ��äơ���CBP�ܢ�BCR��90�� ��BCR�ˤ����ơ���CRB��180�١�90�١�90�٤ˤʤ뤫�顢 CR��BP |
| �̲���͡����٥�� |
| CR��BP��ɤΤ褦�˾������Ƥ����Ф����Τ��� �Ĥޤꡢ��CRB��90�٤�����Ǥ���Ф����Τ����ɡ��������ˡ� ��AQC�ᢤCPB��ޤ��������롣���������ʼ���ͤ��뤳�Ȥ��� ����α��ѥ�٥�ξ����Ǥ��롣 �ݰŵ��Ǥ��뤰�餤�����֤��ƹͤ���С������Υݥ���Ȥ�ή�줬 �����Ƥ��롣 |
| ����ɾ�� |
| ����ľ�Ǥ��뤳�Ȥξ�����3����1ľ����ˤ��뤳�Ȥξ������������� �䤤�ˤ��б��Ǥ���ǽ�Ϥ���2�Τ������ˤ��ᤤ�Ƥ��������� ���������3�Ǥ��ʤ������������˥Х��Х����褦�ǤϤȤƤ� �֤˹��ʤ��Ȼפä��ۤ����褤���ޤ��ޤ����Ǥ�Ф��Ƥ������� ���Ȥ����������뤫�顣 |